振子を二つ、連結して振らせる‥図1。
連結とは、たとえば図でのように、A と B の振れが影響しあうことをいう。
振子は同じ長さと重さをもつ。
いま、A だけを振らせて、B は止まっているとする。 しばらくすると、A の振れは止まり、B が振れるようになる。 もうしばらくすると、再び A が振れるようになり、B は止まる。 こうして、A だけ振れる状態と、B だけ振れる状態が、くり返し交互にあらわれていく。
一見ふしぎな光景には、なにが起きているのだろう。 参考書をひらけば書いてあるはずだけれど、あえてここなりに考えてみよう。
まず、図1の仕掛けを、図2のように置きかえる。 こうしたほうが見やすいし、本質は変らないだろう。 振子を吊るすシャフトには段差*がある。 ここでは段差が小さい、つまり連結の度合いが小さいとする。 そして振子の振れは、あまり大きくならないとしておく。
ひとつの振子を上から見おろすと、その位置は図3のように左右に振れる。 こういう振動の動きは、図4のように表すとよい。 円周上を動点 Q が反時計まわりに等速で移動していて、点の位置の x 座標が、振動の動きを表す。 このとき円の半径は、振動の振幅を定める。 また、ある時刻に円周上のどこに動点があるかが、振動の位相を定める。 つまり、ある規準時刻においてベクトル OQ を書けば、それが振動の状態を表す。
二つの振子が振れるときの、典型的な場面を次のように考えよう。 図5では、A と B が同じ向きに同じ振幅で振れる。 図6では、A と B の振幅は同じだが、互いに逆向きに振れる。 この場面では段差*のぶんだけ、振子が短い。
図5における A と B の振動を、それぞれ表すベクトルを Ap、Bp とすると、それらは長さも向きも等しい‥図7。 そして図6では、振子の振れが逆向きだから、A と B の振動を表す Ax と Bx は、互いに逆を向く‥図8。
ここで、図7が表す振動の動きと、図8が表すその動きを、足し合わせよう。 すると振子 A の振動は Ap + Ax で表されて、倍相当の振幅をもつ。 振子 B については、振動を表す Bp + Bx は打ち消しあってゼロ、つまり動かない。 これは、片方の振子だけが振動している状態、つまり最初の状態を表したことになる。
さて図6にもどると、振子が少し短いから、そのぶん、振動の歩調が少し速い。 図7のうえに図8を重ねて観察すると、Ap と Bp は動かないけれども、Ax と Bx は、ゆっくりと反時計まわりに旋回していく。 ゆっくりとは、たとえば図9のようで、(1)→(2)→(3)へと旋回するあいだには振動のサイクルがたくさん経過する。
では、図7が表す振動の動きに、図9が表す振動の動きを足し合わせよう‥図10。 ベクトル和 Ap + Ax を A とおけば、これが振子 A の振動を表す。 また Bp + Bx を B とおけば、これが振子 B の振動を表す。 時間とともに Ax と Bx が旋回すると、A と B は長さが変わる。 長さは振幅を表すわけだから、これは振幅が増減することを意味する。
はじめに A は*のところで最長であったのが、しだいに縮んでいってゼロになる。 そのとき B は、ゼロから*での最大へと伸びていく。 最大を過ぎたら B は縮んでいって、こんどは A が伸びていく。 二つの振子の振幅が交互に増減するいきさつが、こうして表された。
ベクトル A と B の先端は、直径の両端にあるから、A と B は直角をなす。 言いかえると、振幅が増していくほうの振動は、ちょうど90度だけ位相が遅れる。 このきっちりした関係は、何か意味がありそうだ。
さて、振幅の2乗は、振動のエネルギーに相当する。 (電気の交流では振幅の2乗が電力に相当することを思いおこそう。) 図10を見ると、A の2乗と B の2乗を足せばそれは一定を保つ。 エネルギーの保存が、ちゃんと守られている。
ここまで考えたのは、最初に A が振れて B は止まっている、という特定のケースであった。 では、最初に A も B もあてずっぽうに振らせたら、どうなるだろうか。
それは図11のように、ベクトル A と B をあてずっぽうに置いたことに相当する。 このとき A は Ap + Ax のように、B は Bp + Bx のように分解して表せる。 そして Ap と Bp の組、および Ax と Bx の組に、同じ論法をあてはめてみよう。 するとやはり、A と B の長さが伸び縮みするので、二つの振子の振幅は増減することになる。 ただし振幅がゼロまで減るとは限らないが。
連結振子を、こんな「旋回と伸び縮み」のイメージでとらえると、少しなるほど感がでる ‥だろうか。
いま、A だけを振らせて、B は止まっているとする。 しばらくすると、A の振れは止まり、B が振れるようになる。 もうしばらくすると、再び A が振れるようになり、B は止まる。 こうして、A だけ振れる状態と、B だけ振れる状態が、くり返し交互にあらわれていく。
一見ふしぎな光景には、なにが起きているのだろう。 参考書をひらけば書いてあるはずだけれど、あえてここなりに考えてみよう。
まず、図1の仕掛けを、図2のように置きかえる。 こうしたほうが見やすいし、本質は変らないだろう。 振子を吊るすシャフトには段差*がある。 ここでは段差が小さい、つまり連結の度合いが小さいとする。 そして振子の振れは、あまり大きくならないとしておく。
ひとつの振子を上から見おろすと、その位置は図3のように左右に振れる。 こういう振動の動きは、図4のように表すとよい。 円周上を動点 Q が反時計まわりに等速で移動していて、点の位置の x 座標が、振動の動きを表す。 このとき円の半径は、振動の振幅を定める。 また、ある時刻に円周上のどこに動点があるかが、振動の位相を定める。 つまり、ある規準時刻においてベクトル OQ を書けば、それが振動の状態を表す。
二つの振子が振れるときの、典型的な場面を次のように考えよう。 図5では、A と B が同じ向きに同じ振幅で振れる。 図6では、A と B の振幅は同じだが、互いに逆向きに振れる。 この場面では段差*のぶんだけ、振子が短い。
図5における A と B の振動を、それぞれ表すベクトルを Ap、Bp とすると、それらは長さも向きも等しい‥図7。 そして図6では、振子の振れが逆向きだから、A と B の振動を表す Ax と Bx は、互いに逆を向く‥図8。
ここで、図7が表す振動の動きと、図8が表すその動きを、足し合わせよう。 すると振子 A の振動は Ap + Ax で表されて、倍相当の振幅をもつ。 振子 B については、振動を表す Bp + Bx は打ち消しあってゼロ、つまり動かない。 これは、片方の振子だけが振動している状態、つまり最初の状態を表したことになる。
さて図6にもどると、振子が少し短いから、そのぶん、振動の歩調が少し速い。 図7のうえに図8を重ねて観察すると、Ap と Bp は動かないけれども、Ax と Bx は、ゆっくりと反時計まわりに旋回していく。 ゆっくりとは、たとえば図9のようで、(1)→(2)→(3)へと旋回するあいだには振動のサイクルがたくさん経過する。
では、図7が表す振動の動きに、図9が表す振動の動きを足し合わせよう‥図10。 ベクトル和 Ap + Ax を A とおけば、これが振子 A の振動を表す。 また Bp + Bx を B とおけば、これが振子 B の振動を表す。 時間とともに Ax と Bx が旋回すると、A と B は長さが変わる。 長さは振幅を表すわけだから、これは振幅が増減することを意味する。
はじめに A は*のところで最長であったのが、しだいに縮んでいってゼロになる。 そのとき B は、ゼロから*での最大へと伸びていく。 最大を過ぎたら B は縮んでいって、こんどは A が伸びていく。 二つの振子の振幅が交互に増減するいきさつが、こうして表された。
ベクトル A と B の先端は、直径の両端にあるから、A と B は直角をなす。 言いかえると、振幅が増していくほうの振動は、ちょうど90度だけ位相が遅れる。 このきっちりした関係は、何か意味がありそうだ。
さて、振幅の2乗は、振動のエネルギーに相当する。 (電気の交流では振幅の2乗が電力に相当することを思いおこそう。) 図10を見ると、A の2乗と B の2乗を足せばそれは一定を保つ。 エネルギーの保存が、ちゃんと守られている。
ここまで考えたのは、最初に A が振れて B は止まっている、という特定のケースであった。 では、最初に A も B もあてずっぽうに振らせたら、どうなるだろうか。
それは図11のように、ベクトル A と B をあてずっぽうに置いたことに相当する。 このとき A は Ap + Ax のように、B は Bp + Bx のように分解して表せる。 そして Ap と Bp の組、および Ax と Bx の組に、同じ論法をあてはめてみよう。 するとやはり、A と B の長さが伸び縮みするので、二つの振子の振幅は増減することになる。 ただし振幅がゼロまで減るとは限らないが。
連結振子を、こんな「旋回と伸び縮み」のイメージでとらえると、少しなるほど感がでる ‥だろうか。
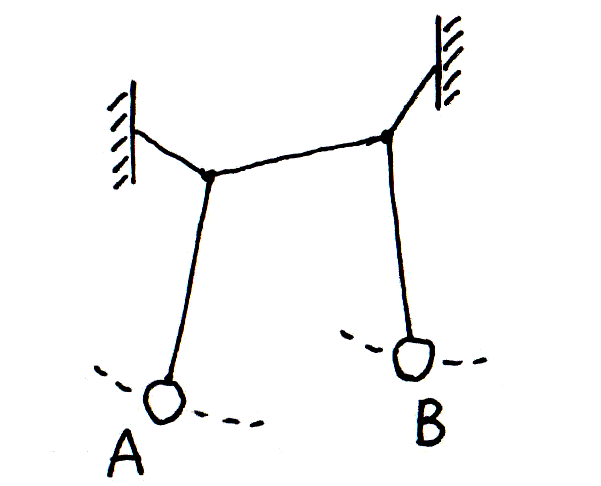 図1
図1 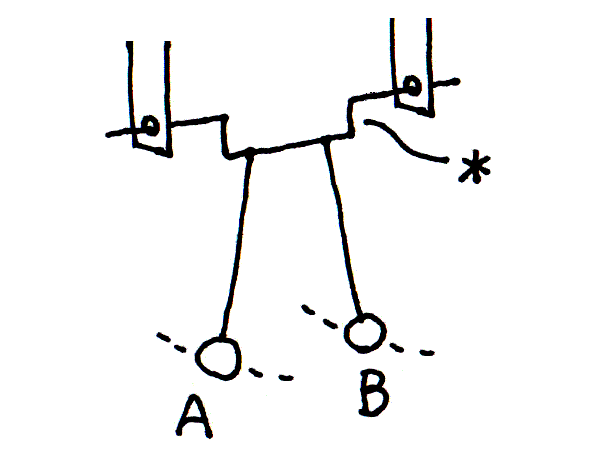 図2
図2 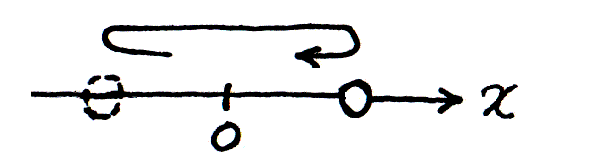 図3
図3 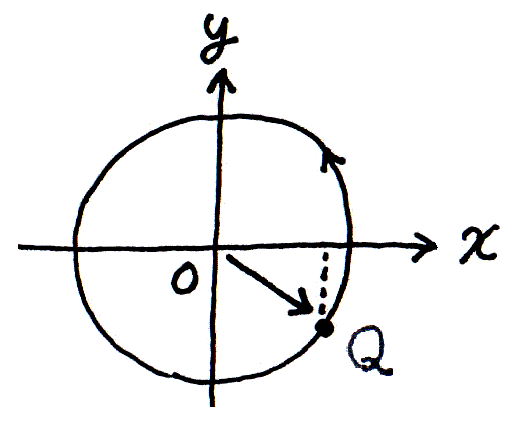 図4
図4 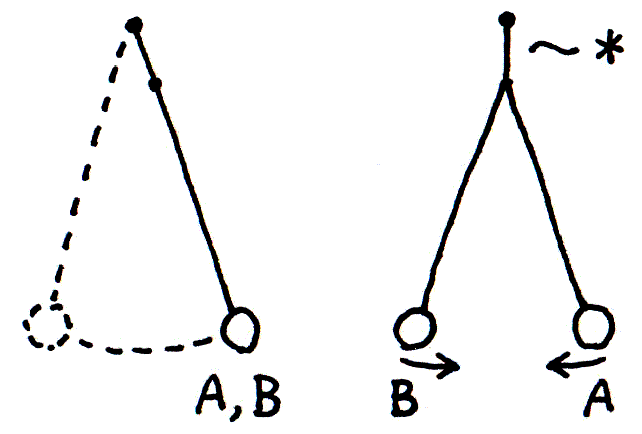
図5 図6
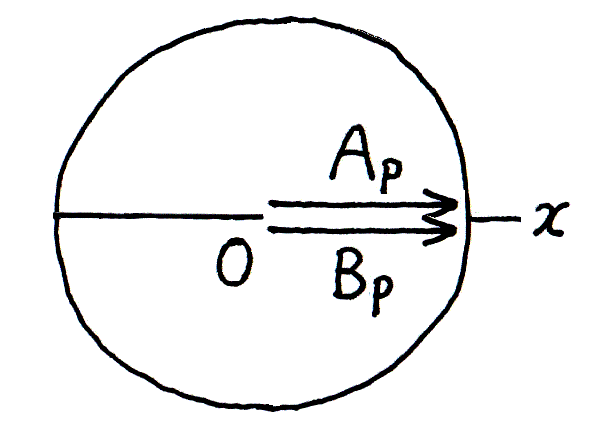 図7
図7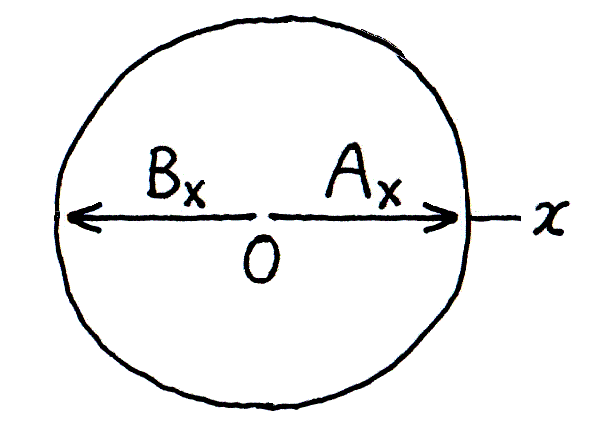 図8
図8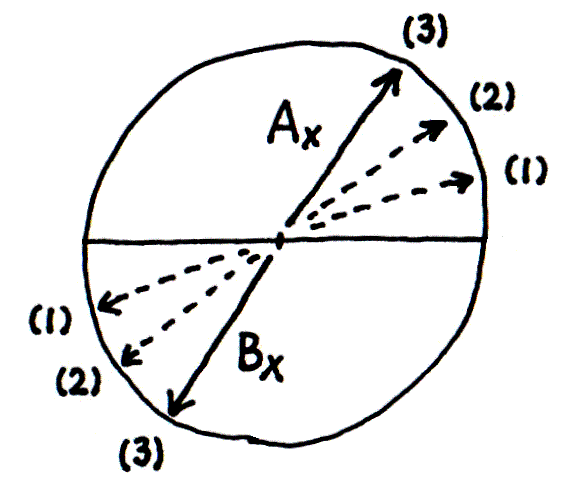 図9
図9 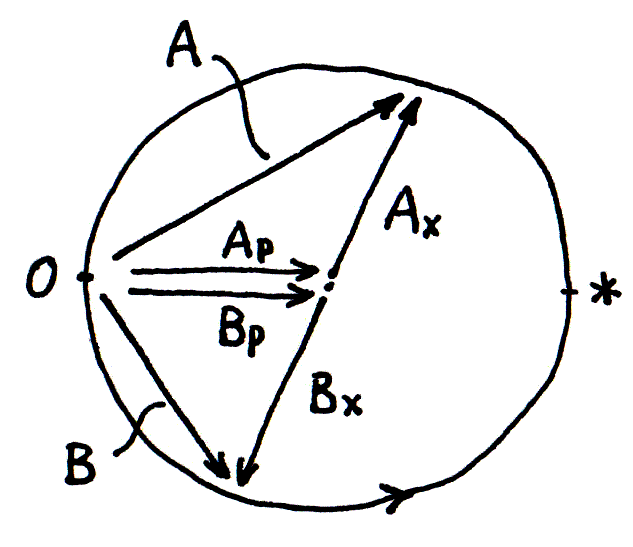
図10
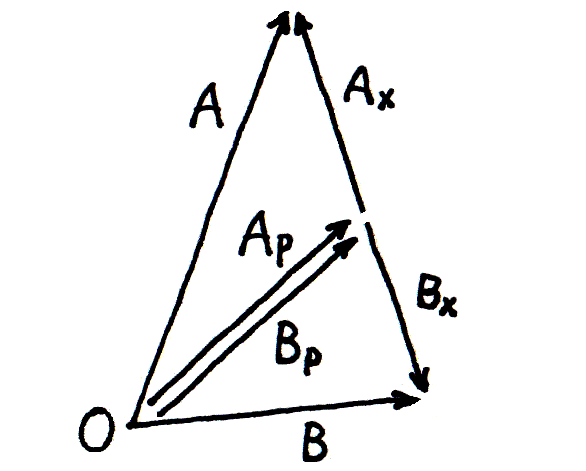
図11
目次へ戻る