回旋塔の基本は、図1のようであった。
まずAのように開き角 θ を限度いっぱいにとって、円速度で助走する。
そしてBのように、足をちぢめて円錐運動をおこなう。
さて自分自身の記憶によれば、足をちぢめたりしなくても、足先が地面をこすることなく円錐運動をできる場合があった。 それは一体どういう場合だったのだろうか。 (記憶はたぶん違っていない。足先を地面につけたくても届かなかったのを覚えている。)
自分は背丈が小さかったので、助走の開き角は図2のAのように小さめになる(Bは大きい子。) ここでは小さい子がひとり、大きい子たちの中にまざったとしよう。
いっせいに助走をすると、Aの助走円はBのそれよりも小さい。 そして円錐運動に入って柱をまわる角速度は、BよりもAのほうが小さい。 なのでAのまわるうごきは、Bに遅れをとることになる。
ここで鎖の支点は、一点に固定されるのでなく、自由にまわる小円盤の周上に並んでいることを思いだす。 Bは人数が多いから、円盤はBの角速度に合わせてまわるとしてよい。 すると円盤とAの関係は図3のようになり、円盤に対してAは遅れ角 φ をもつ(図は平面図)。 鎖がAを引きよせる力を平面図上で f と置けば、小さい係数 ε をかけた εf という力が、Aを少し加速するようにはたらく。 加速されるとAの開き角はだんだん増していって、やがてBの開き角に一致するであろう(そして遅れ角 φ はゼロになる。) そうなれば、背丈が小さいAは、たとえ足を伸ばしても地面にとどかない。
要するにAは、Bに引っ張ってもらうことで、Bとおなじ開き角に達する。 ちゃっかり便乗組というわけだ。
けれども力 εf には、そういう効力が本当にあるだろうか。 ためしに図3にて、円盤の半径を30cm、Aの回転半径を2mと置き、遅れ角 φ は30度くらいとすると、
ε = 0.09
となる。 このときAの開き角はどうなるか。
円錐運動は図4のように定まる。 振り子は単位質量をもつと置けば、それにはたらく遠心力
f = Ω2 R sinθ
と、重力 g とが、R の垂線に沿ってつりあう。(図4と図3の f の関係に注意。) このことから角速度は
Ω = √ g / R / √ cosθ
と定まる。 開き角 θ は大きくないとすると、円速度 v は近似的に
v = Ω R sinθ = θ √ g R
となる。 よって速度 v と開き角 θ のあいだに、変化関係
Δθ = Δv / √ g R
が成りたつ。
さて力 εf は、時間 Δt のあいだに速度変化をつぎのようにひきおこす。
Δv = εf Δt = ε R θ Ω2 Δt = ε θ g Δt
ただし Ω2=g/R とした。 ともなって開き角は
Δθ = ε θ Ω Δt
だけ増す。 いま仮りに θ=0.5 くらいにあるとしよう。 円錐運動が1周するあいだの θ の増し高をみるために、ΩΔt=2π とおけば、
Δθ = π ε = 180° ε = 16°
を得る。 大まかな見積もりだが、1周するあいだに開き角は目に見えて増す。 ほんの数周のうちに、Aの開き角はBに並ぶであろう。
こうして便乗組は円錐運動を楽しめたのであった。
さて自分自身の記憶によれば、足をちぢめたりしなくても、足先が地面をこすることなく円錐運動をできる場合があった。 それは一体どういう場合だったのだろうか。 (記憶はたぶん違っていない。足先を地面につけたくても届かなかったのを覚えている。)
自分は背丈が小さかったので、助走の開き角は図2のAのように小さめになる(Bは大きい子。) ここでは小さい子がひとり、大きい子たちの中にまざったとしよう。
いっせいに助走をすると、Aの助走円はBのそれよりも小さい。 そして円錐運動に入って柱をまわる角速度は、BよりもAのほうが小さい。 なのでAのまわるうごきは、Bに遅れをとることになる。
ここで鎖の支点は、一点に固定されるのでなく、自由にまわる小円盤の周上に並んでいることを思いだす。 Bは人数が多いから、円盤はBの角速度に合わせてまわるとしてよい。 すると円盤とAの関係は図3のようになり、円盤に対してAは遅れ角 φ をもつ(図は平面図)。 鎖がAを引きよせる力を平面図上で f と置けば、小さい係数 ε をかけた εf という力が、Aを少し加速するようにはたらく。 加速されるとAの開き角はだんだん増していって、やがてBの開き角に一致するであろう(そして遅れ角 φ はゼロになる。) そうなれば、背丈が小さいAは、たとえ足を伸ばしても地面にとどかない。
要するにAは、Bに引っ張ってもらうことで、Bとおなじ開き角に達する。 ちゃっかり便乗組というわけだ。
けれども力 εf には、そういう効力が本当にあるだろうか。 ためしに図3にて、円盤の半径を30cm、Aの回転半径を2mと置き、遅れ角 φ は30度くらいとすると、
ε = 0.09
となる。 このときAの開き角はどうなるか。
円錐運動は図4のように定まる。 振り子は単位質量をもつと置けば、それにはたらく遠心力
f = Ω2 R sinθ
と、重力 g とが、R の垂線に沿ってつりあう。(図4と図3の f の関係に注意。) このことから角速度は
Ω = √ g / R / √ cosθ
と定まる。 開き角 θ は大きくないとすると、円速度 v は近似的に
v = Ω R sinθ = θ √ g R
となる。 よって速度 v と開き角 θ のあいだに、変化関係
Δθ = Δv / √ g R
が成りたつ。
さて力 εf は、時間 Δt のあいだに速度変化をつぎのようにひきおこす。
Δv = εf Δt = ε R θ Ω2 Δt = ε θ g Δt
ただし Ω2=g/R とした。 ともなって開き角は
Δθ = ε θ Ω Δt
だけ増す。 いま仮りに θ=0.5 くらいにあるとしよう。 円錐運動が1周するあいだの θ の増し高をみるために、ΩΔt=2π とおけば、
Δθ = π ε = 180° ε = 16°
を得る。 大まかな見積もりだが、1周するあいだに開き角は目に見えて増す。 ほんの数周のうちに、Aの開き角はBに並ぶであろう。
こうして便乗組は円錐運動を楽しめたのであった。
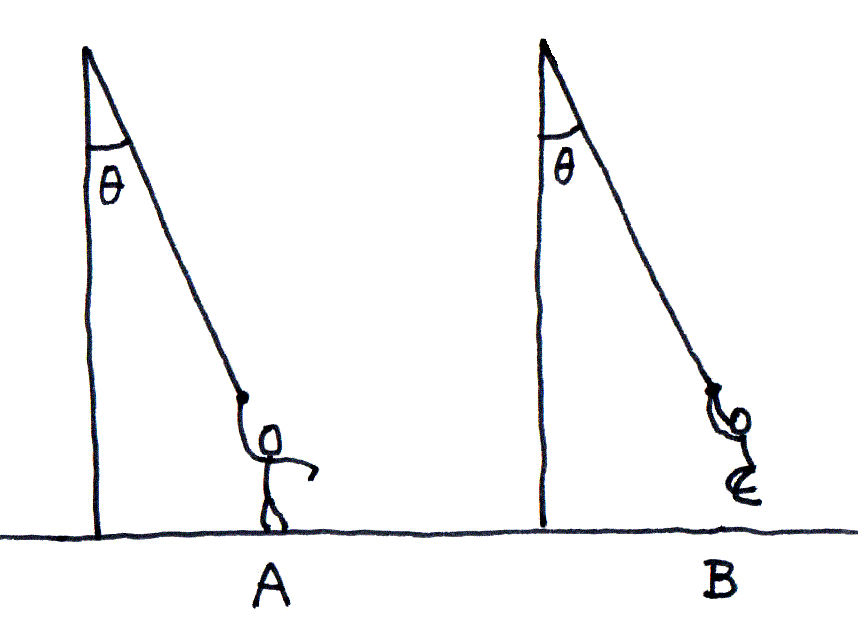
図1
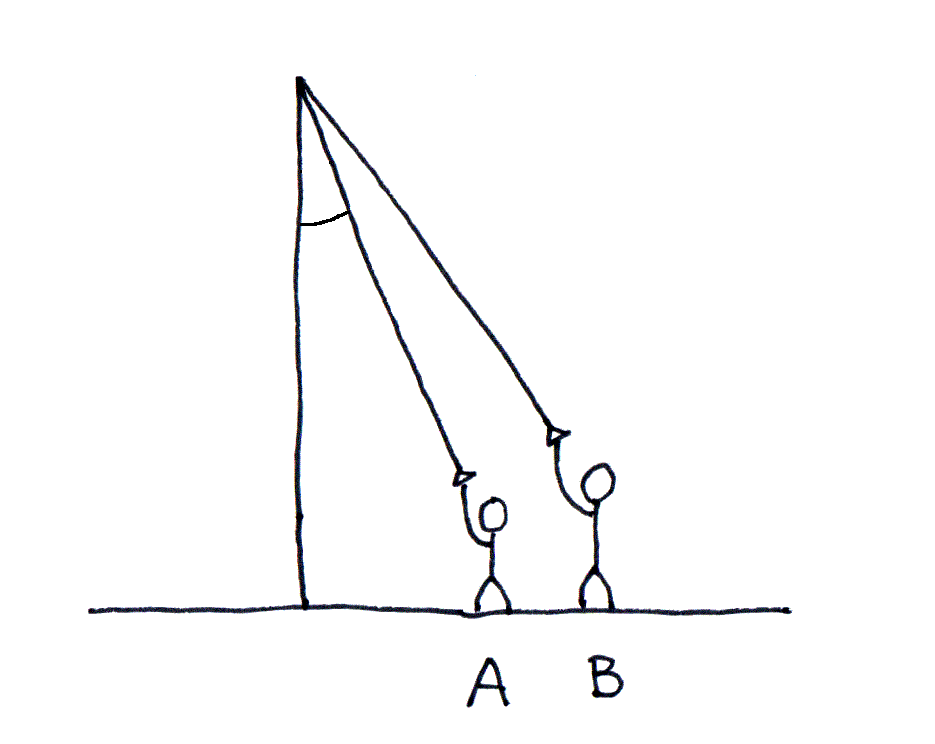
図2
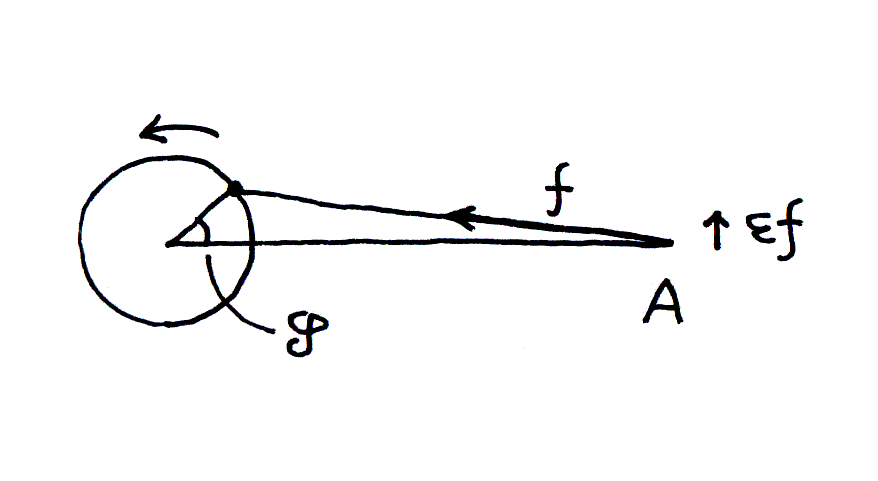
図3
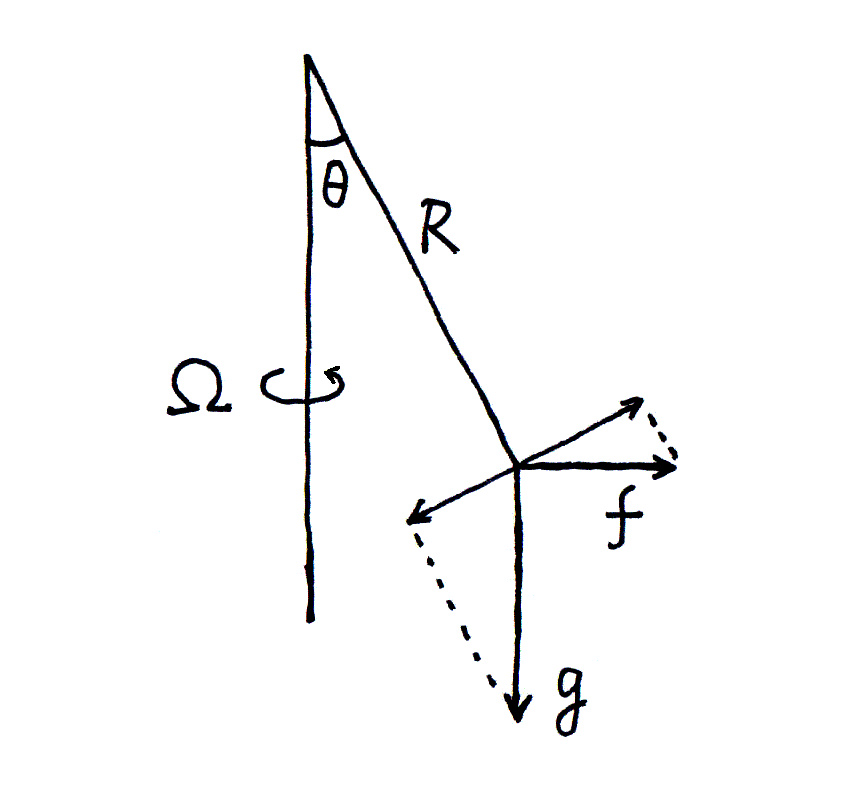
図4
目次へ戻る